Neural Machine Translation with Attention¶
If you wanna read more about this type of Machine Translation, Wikipedia is a good source.
This notebook has been inspited by the Deeplearning.ai - Sequence models course - Attention mechanism.
The idea is to build a Neural Machine Translation (NMT) model to translate human readable dates ("10th of September, 1978") into machine readable dates ("1978-09-10"), using attention model.
Attention mechanism¶
If you had to translate a book's paragraph from French to English, you would not read the whole paragraph, then close the book and translate. Even during the translation process, you would read/re-read and focus on the parts of the French paragraph corresponding to the parts of the English you are writing down.
The attention mechanism tells a Neural Machine Translation model where it should pay attention to at any step. Andrew Ng explains this mechanism quite well in these tho videos: Attention model intuition and Attention model
Here is a figure to remind you how the model works. The diagram on the left shows the attention model:
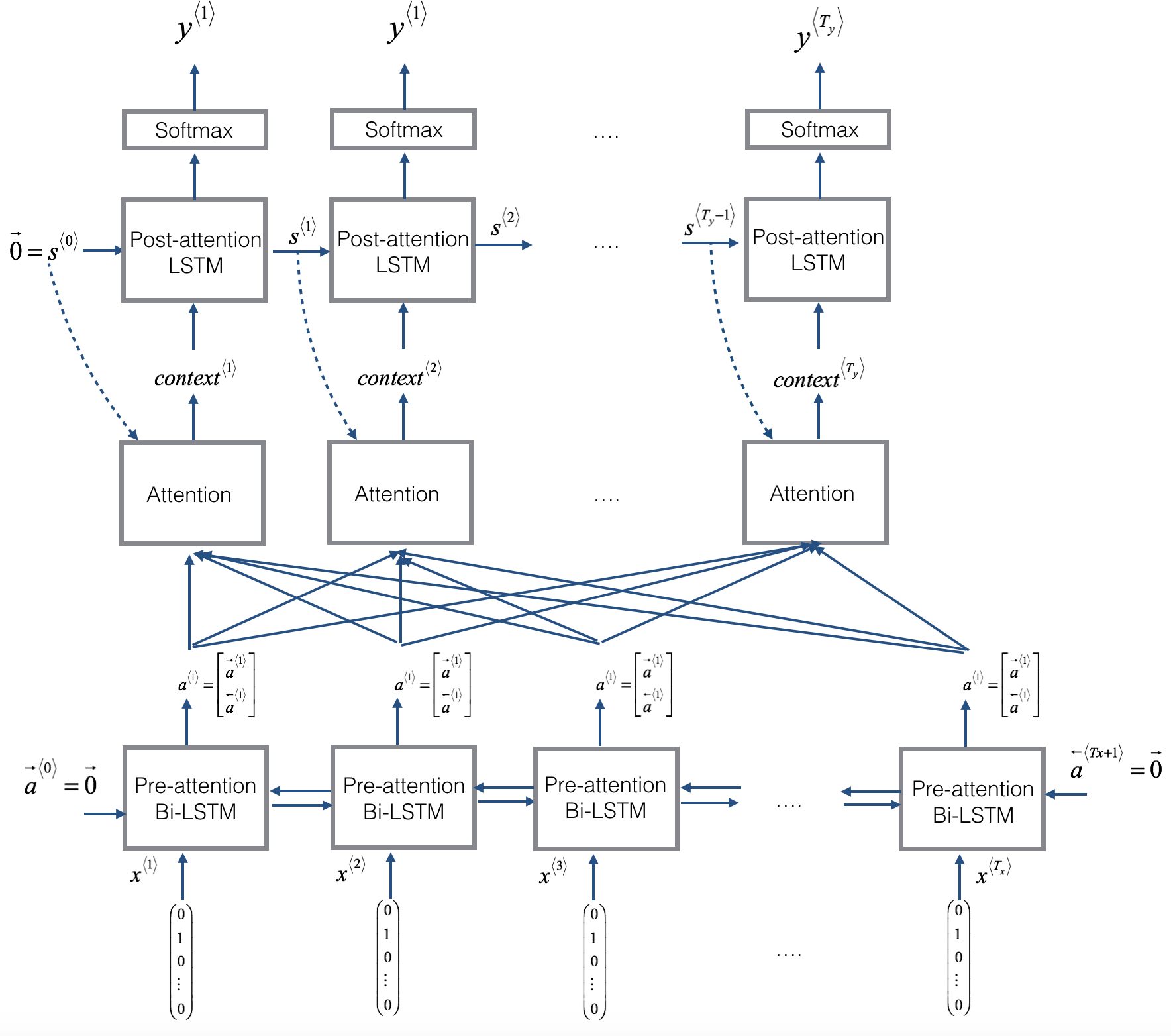 |
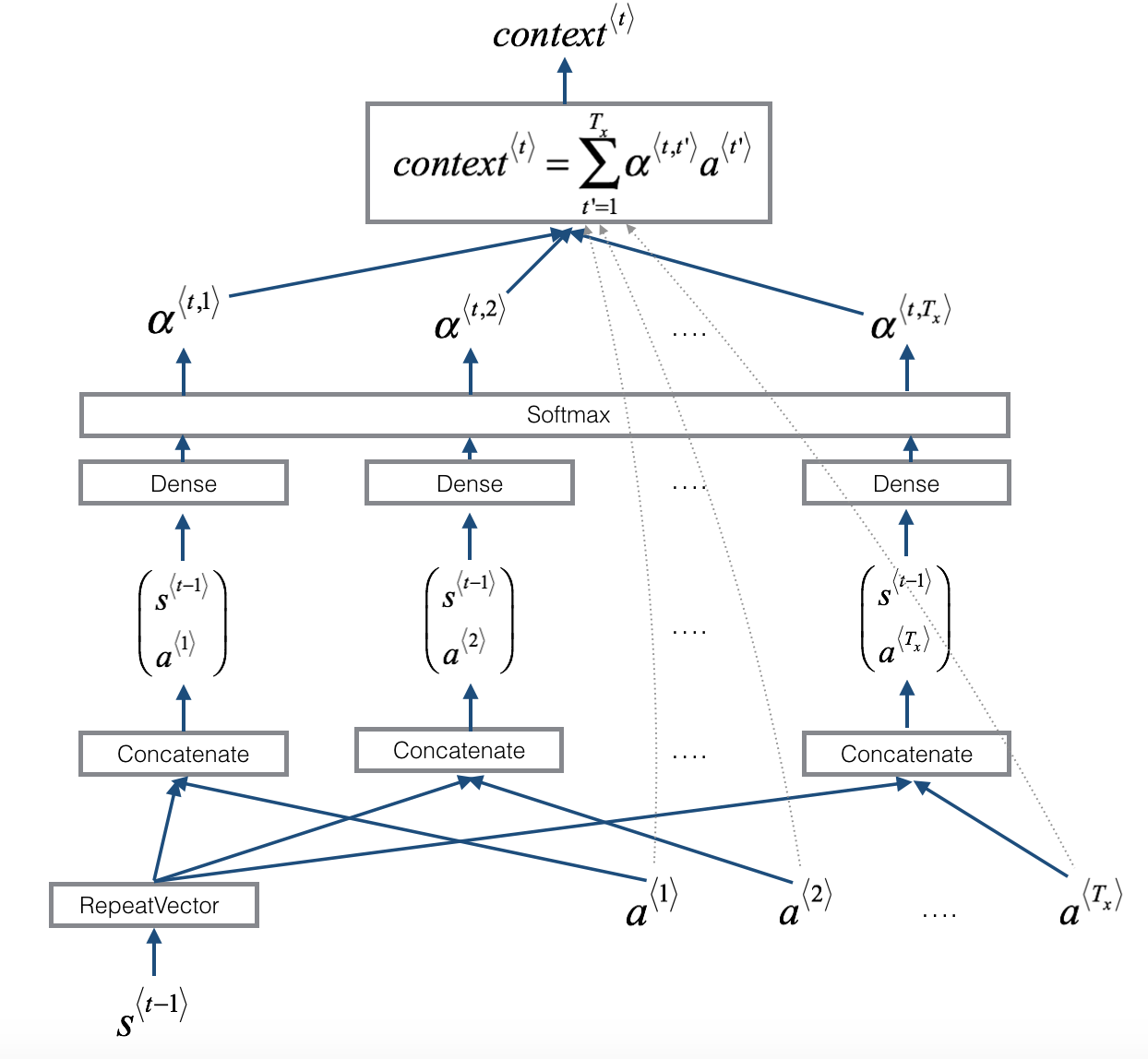 |
Here are some properties of the model:
There are two separate LSTMs in this model (see diagram on the left). Because the one at the bottom of the picture is a Bi-directional LSTM and comes before the attention mechanism, we will call it pre-attention Bi-LSTM. The LSTM at the top of the diagram comes after the attention mechanism, so we will call it the post-attention LSTM. The pre-attention Bi-LSTM goes through $T_x$ time steps; the post-attention LSTM goes through $T_y$ time steps.
The post-attention LSTM passes $s^{\langle t \rangle}, c^{\langle t \rangle}$ from one time step to the next. The LSTM has both the output activation $s^{\langle t\rangle}$ and the hidden cell state $c^{\langle t\rangle}$. In this model the post-activation LSTM at time $t$ does will not take the specific generated $y^{\langle t-1 \rangle}$ as input; it only takes $s^{\langle t\rangle}$ and $c^{\langle t\rangle}$ as input. We have designed the model this way, because (unlike language generation where adjacent characters are highly correlated) there isn't as strong a dependency between the previous character and the next character in a YYYY-MM-DD date.
We use $a^{\langle t \rangle} = [\overrightarrow{a}^{\langle t \rangle}; \overleftarrow{a}^{\langle t \rangle}]$ to represent the concatenation of the activations of both the forward-direction and backward-directions of the pre-attention Bi-LSTM.
The diagram on the right uses a
RepeatVectornode to copy $s^{\langle t-1 \rangle}$'s value $T_x$ times, and thenConcatenationto concatenate $s^{\langle t-1 \rangle}$ and $a^{\langle t \rangle}$ to compute $e^{\langle t, t'}$, which is then passed through a softmax to compute $\alpha^{\langle t, t' \rangle}$. We'll explain how to useRepeatVectorandConcatenationin Keras below.
Let's begin importing the necessary packages:
from keras.layers import Bidirectional, Concatenate, Permute, Dot, Input, LSTM, Multiply
from keras.layers import RepeatVector, Dense, Activation, Lambda
from keras.optimizers import Adam
from keras.utils import to_categorical
from keras.models import load_model, Model
import keras.backend as K
import numpy as np
from faker import Faker
import random
from tqdm import tqdm
from babel.dates import format_date
import matplotlib.pyplot as plt
%matplotlib inline
Step1: Generate Dataset¶
Following we'll use Faker to generate our own dataset of human readable date with their iso format (machine readable date) as labels.
fake = Faker()
# We need to seed these guys. For some reason I always use 101
fake.seed(101)
random.seed(101)
We're gonna generate a dataset with different formats. In this case I'm giving more chances to the most humman readable formats.
FORMATS = ['short', # d/M/YY
'medium', # MMM d, YYY
'medium',
'medium',
'long', # MMMM dd, YYY
'long',
'long',
'long',
'long',
'full', # EEEE, MMM dd, YYY
'full',
'full',
'd MMM YYY',
'd MMMM YYY',
'd MMMM YYY',
'd MMMM YYY',
'd MMMM YYY',
'd MMMM YYY',
'dd/MM/YYY',
'EE d, MMM YYY',
'EEEE d, MMMM YYY']
Let's have a look at those formats:
for format in FORMATS:
print('%s => %s' %(format, format_date(fake.date_object(), format=format, locale='en')))
random_date() will generate a random date using a random format picked from our list FORMATS defined before. It'll return a tuple with the human and machine readable date plus the date object:
def random_date():
dt = fake.date_object()
try:
date = format_date(dt, format=random.choice(FORMATS), locale='en')
human_readable = date.lower().replace(',', '')
machine_readable = dt.isoformat()
except AttributeError as e:
return None, None, None
return human_readable, machine_readable, dt
create_dataset(m) will generate our dataset, taking m as the number of samples to create. It returns the dataset as a list, two dictionaries mapping index to character (these are our vocabularies), human and machine, and the inverse mapping, inv_machine, chars to index:
def create_dataset(m):
human_vocab = set()
machine_vocab = set()
dataset = []
for i in tqdm(range(m)):
h, m, _ = random_date()
if h is not None:
dataset.append((h, m))
human_vocab.update(tuple(h))
machine_vocab.update(tuple(m))
# We also add two special chars, <unk> for unknown characters, and <pad> to add padding at the end
human = dict(zip(sorted(human_vocab) + ['<unk>', '<pad>'], list(range(len(human_vocab) + 2))))
inv_machine = dict(enumerate(sorted(machine_vocab)))
machine = {v: k for k, v in inv_machine.items()}
return dataset, human, machine, inv_machine
Let's generate a dataset with 30k samples. That's probably way too much, but it should do a good job:
m = 30000
dataset, human_vocab, machine_vocab, inv_machine_vocab = create_dataset(m)
Inspecting the first 10 entries. Remember it contains a list of tuples => (human readable, machine readable):
dataset[:10]
Let's have a look at our human readable vocabulary:
human_vocab
Machine readable vocabulary:
machine_vocab
... and its inverse dictionary:
inv_machine_vocab
Step 2: Preprocessing¶
preprocess_data(dataset, human_vocab, machine_vocab, Tx, Ty) is gonna do some beautiful magic with our dataset. It takes the whole dataset, and both human and machine vocabularie, plus some max length arguments, and it'll spit out out training set and target labels, plus the one hot encoding of both:
def preprocess_data(dataset, human_vocab, machine_vocab, Tx, Ty):
X, Y = zip(*dataset)
X = np.array([string_to_int(i, Tx, human_vocab) for i in X])
Y = [string_to_int(t, Ty, machine_vocab) for t in Y]
Xoh = np.array(list(map(lambda x: to_categorical(x, num_classes=len(human_vocab)), X)))
Yoh = np.array(list(map(lambda x: to_categorical(x, num_classes=len(machine_vocab)), Y)))
return X, np.array(Y), Xoh, Yoh
string_to_int(string, length, vocab) will return a list of indexes based on a string and vocabulary, vocab, cropping or padding it depending on the max length passed in:
def string_to_int(string, length, vocab):
string = string.lower()
string = string.replace(',','')
if len(string) > length:
string = string[:length]
rep = list(map(lambda x: vocab.get(x, '<unk>'), string))
if len(string) < length:
rep += [vocab['<pad>']] * (length - len(string))
return rep
Let's have a look at an example. By the way, that's my birthday 😉:
string_to_int('September 10, 1978', 30, human_vocab)
Let's run the preprocessing and print out some shapes:
Tx = 30
Ty = 10
X, Y, Xoh, Yoh = preprocess_data(dataset, human_vocab, machine_vocab, Tx, Ty)
print("X.shape:", X.shape)
print("Y.shape:", Y.shape)
print("Xoh.shape:", Xoh.shape)
print("Yoh.shape:", Yoh.shape)
... and see what a training sample, target label and their respective one hot encoding look like:
index = 0
print("Source date:", dataset[index][0])
print("Target date:", dataset[index][1])
print()
print("Source after preprocessing (indices):", X[index])
print("Target after preprocessing (indices):", Y[index])
print()
print("Source after preprocessing (one-hot):", Xoh[index])
print("Target after preprocessing (one-hot):", Yoh[index])
This is what we have now:
X: a processed version of the human readable dates in the training set, where each character is replaced by an index mapped to the character via human_vocab. Each date is further padded to
Txvalues with a special character<pad>.X.shape = (m, Tx)Y: a processed version of the machine readable dates in the training set, where each character is replaced by the index it is mapped to in machine_vocab. You should have
Y.shape = (m, Ty).Xoh: one-hot version of X, the "1" entry's index is mapped to the character thanks to human_vocab.
Xoh.shape = (m, Tx, len(human_vocab)).Yoh: one-hot version of Y, the "1" entry's index is mapped to the character thanks to machine_vocab.
Yoh.shape = (m, Tx, len(machine_vocab)). Here,len(machine_vocab) = 11since there are 11 characters ('-' as well as 0-9).
Step 3: Define Model¶
Let's define some layers we need as global variables. RepeatVector(), Concatenate(), Dense(), Activation(), Dot()
repeator = RepeatVector(Tx)
concatenator = Concatenate(axis=-1)
densor1 = Dense(10, activation = "tanh")
densor2 = Dense(1, activation = "relu")
activator = Activation('softmax', name='attention_weights')
dotor = Dot(axes = 1)
one_step_attention(a, s_prev): At step $t$, given all the hidden states of the Bi-LSTM ($[a^{<1>},a^{<2>}, ..., a^{<T_x>}]$) and the previous hidden state of the second LSTM ($s^{<t-1>}$), one_step_attention() will compute the attention weights ($[\alpha^{<t,1>},\alpha^{<t,2>}, ..., \alpha^{<t,T_x>}]$) and output the context vector:
$$context^{<t>} = \sum_{t' = 0}^{T_x} \alpha^{<t,t'>}a^{<t'>}\tag{1}$$
def one_step_attention(a, s_prev):
s_prev = repeator(s_prev)
concat = concatenator([a, s_prev])
e = densor1(concat)
energies = densor2(e)
alphas = activator(energies)
context = dotor([alphas, a])
return context
n_a = 32
n_s = 64
post_activation_LSTM_cell = LSTM(n_s, return_state = True)
output_layer = Dense(len(machine_vocab), activation='softmax')
model(Tx, Ty, n_a, n_s, human_vocab_size, machine_vocab_size): Implements the entire model. It first runs the input through a Bidirectional LSTM to get back $[a^{<1>},a^{<2>}, ..., a^{<T_x>}]$. Then, it calls one_step_attention() $T_y$ times (for loop). At each iteration of this loop, it gives the computed context vector $c^{<t>}$ to the second LSTM, and runs the output of the LSTM through a dense layer with softmax activation to generate a prediction $\hat{y}^{<t>}$.
def model(Tx, Ty, n_a, n_s, human_vocab_size, machine_vocab_size):
X = Input(shape=(Tx, human_vocab_size))
s0 = Input(shape=(n_s,), name='s0')
c0 = Input(shape=(n_s,), name='c0')
s = s0
c = c0
outputs = []
a = Bidirectional(LSTM(n_a, return_sequences = True))(X)
for t in range(Ty):
context = one_step_attention(a, s)
s, _, c = post_activation_LSTM_cell(context, initial_state=[s, c])
out = output_layer(s)
outputs.append(out)
model = Model([X, s0, c0], outputs)
return model
Model instantiation and summary representation of the model:
mod = model(Tx, Ty, n_a, n_s, len(human_vocab), len(machine_vocab))
mod.summary()
Step 4: Train Model¶
Using Adam optimizer we proceed to compile and train our model:
opt = Adam(lr=0.005, beta_1=0.9, beta_2=0.999, decay=0.01)
mod.compile(optimizer=opt, loss='categorical_crossentropy', metrics=['accuracy'])
s0 = np.zeros((m, n_s))
c0 = np.zeros((m, n_s))
outputs = list(Yoh.swapaxes(0,1))
mod.fit([Xoh, s0, c0], outputs, epochs=30, batch_size=100)
Step 5: Testing Model (optional)¶
We could perform more serious testing and evaluation of the model here, but since we didn't do a proper train/test split we'll just make some predictions to see whether it gets them right:
EXAMPLES = ['3 May 1979', '5 April 09', '21th of August 2016', 'Tue 10 Jul 2007', 'Saturday May 9 2018', 'March 3 2001', 'March 3rd 2001', '1 March 2001']
for example in EXAMPLES:
source = string_to_int(example, Tx, human_vocab)
source = np.array(list(map(lambda x: to_categorical(x, num_classes=len(human_vocab)), source)))
source = source.reshape((1, ) + source.shape)
prediction = mod.predict([source, s0, c0])
prediction = np.argmax(prediction, axis = -1)
output = [inv_machine_vocab[int(i)] for i in prediction]
print("source:", example)
print("output:", ''.join(output))
Step 6: Save and convert Model¶
Finally we save the model to be converted and used by our Frontend component using TensorFlow.js. Conversion will be done outside this notebook.
mod.save('dates_model.h5')
!tensorflowjs_converter --input_format keras dates_model.h5 tfjsmodel